波流共同作用下的海滩剖面演变数学模型(CROss-shore Sediment Transport and Profile Evolution Model, CROSPE)由河海大学海岸整治修复研究团队张弛教授等人研发。本模型的研发和改进得到国家自然科学基金面上项目(51879096)、青年项目(51209082)和江苏省自然科学基金面上项目(BK20161509)等项目的支持。
CROSPE可以模拟风暴和常浪等不同条件下的波浪传播变形、波生流分布、泥沙向/离岸输运、海滩侵蚀/恢复等剖面形态演变,也可用于海滩养护修复工程中不同填沙粒径、填沙坡度和不同重现期波浪作用下的人工沙滩剖面演变预测。
欢迎感兴趣的科研人员共同优化CROSPE,有关CROSPE具体信息或模型应用可联系张弛教授zhangchi@hhu.edu.cn或李元博士生yuanli@hhu.edu.cn。
模型框架:
(1)波浪模块:采用波能守恒方程模拟波浪浅化、破碎和再恢复等传播变形过程;
(2)破波水滚模块:采用水滚能量平衡方程模拟破波水滚的成长与耗散过程;
(3)底部离岸流模块:采用质量守恒方程和 Boussinesq 假定模拟底部离岸流的流速及其垂向分布;
(4)波流边界层模块:采用动量守恒方程模拟近底边界层流速剖面和床面剪切应力的周期内变化;
(5)泥沙运动模块:采用悬移质对流扩散方程模拟含沙量的时空分布,基于希尔兹参数计算推移质输沙率,可以考虑不均匀泥沙运动;
(6)地形演变模块:根据输沙率沿程梯度,采用 Euler-WENO 格式计算床面高程变化。
模型特点:
(1)求解水深解析和相位解析的波流边界层动量守恒方程,可以较好地描述流速、含沙量和输沙率的水深变化特性与相位变化特性;
(2)采用一个非线性波浪振荡速度经验计算公式,作为波浪压强梯度项的输入条件,同时考虑了波浪的速度不对称性和加速度不对称性;
(3)在动量守恒方程中引入了底部离岸流引起的时均水平压强梯度项,更好描述了非线性波浪和底部离岸流的相互作用;
(4)建立了新的时变紊动涡粘系数公式,反映近底流速与紊动之间的相位滞后效应,改进了常浪条件下向岸推移质输沙的计算精度;
(5)通过引入两个校正系数,考虑非均匀沙颗粒之间的隐蔽/暴露影响,修正非均匀泥沙在波流作用下所受的剪切应力及临界剪切应力计算,使模型在计算非均匀沙海滩剖面演变的同时,可以模拟海滩剖面上的各点的粒径变化。
计算机软件著作权:
波流共同作用下海滩剖面演变数值计算软件(HHU-CROSPE),登记号2012SR122136,著作权人:河海大学,国家版权局。
模型评价:
发表在Journal of Waterway, Port, Coastal and Ocean Engineering – ASCE期刊上的CROSPE模型研究成果“Numerical Study of Sandbar Migration under Wave-Undertow Interaction”,获得该期刊2014年度的最佳论文奖(Best Journal Paper Award)。
正在开展的模型改进:
(1)修正波浪非线性参数与破碎指标表达式使之适用于更广泛的波浪与地形条件,改进水滚能量耗散表达式和水滚坡度等关键物理参数的确定方法,以更好刻画水深剧烈变化条件下的非稳态演化特征。
(2)使用新的物模实验数据对数学模型进行验证,考察模型针对人工沙坝向岸移动和形态演变过程的定量模拟精度,据此优化计算方法使之更适用于人工沙坝喂养海滩的模拟。
(3)收集更多的现场实测数据验证优化模型。
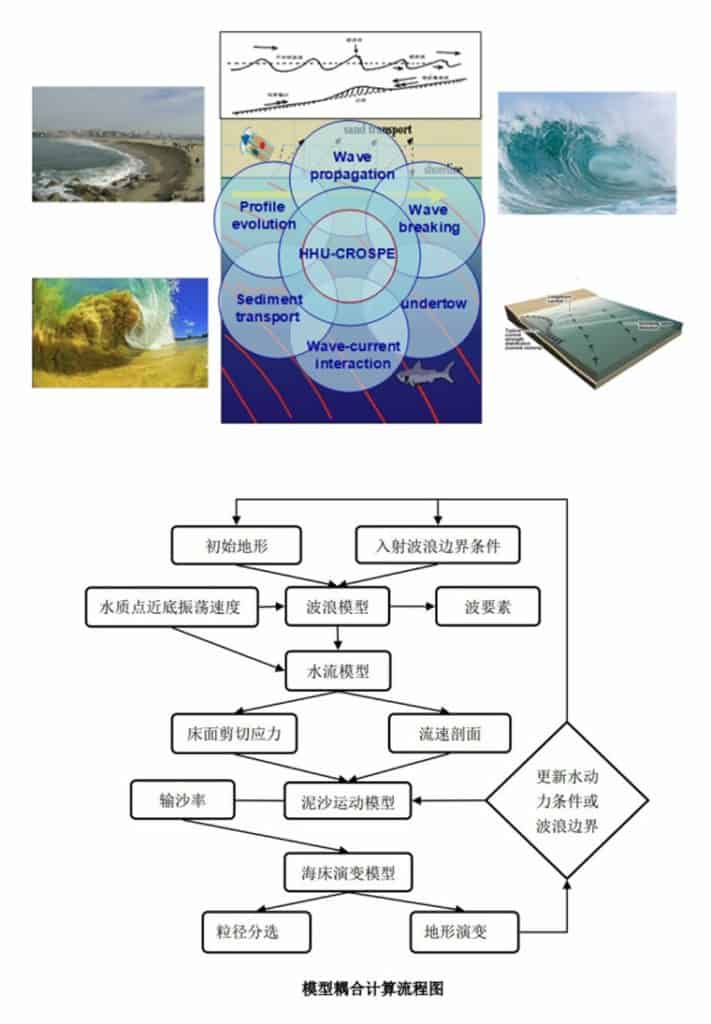
图1 CROSPE模型框架和计算流程示意图
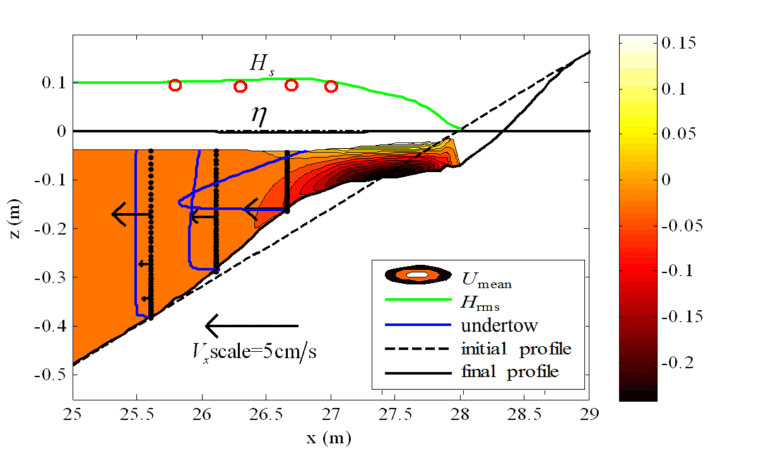
图2 波浪传播变形与波生流场模拟
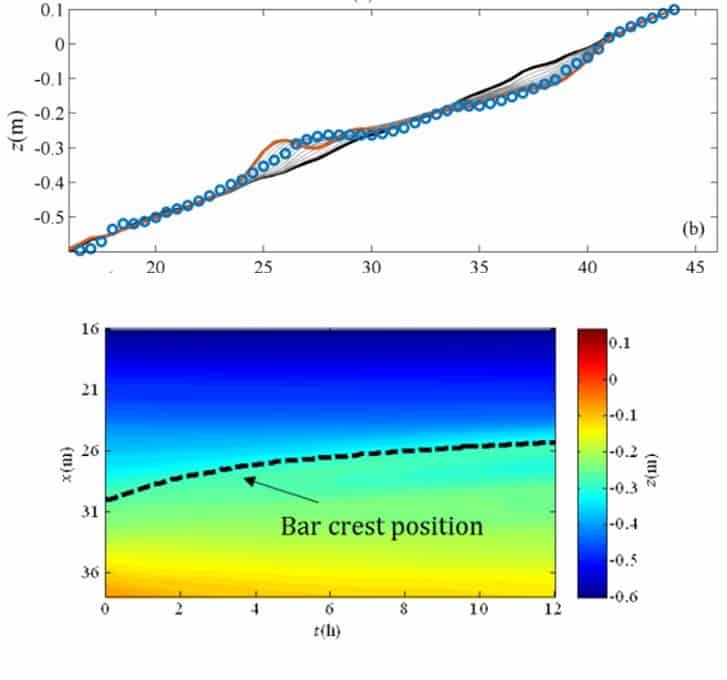
图3 风暴作用下的海滩剖面演变及平衡剖面模拟
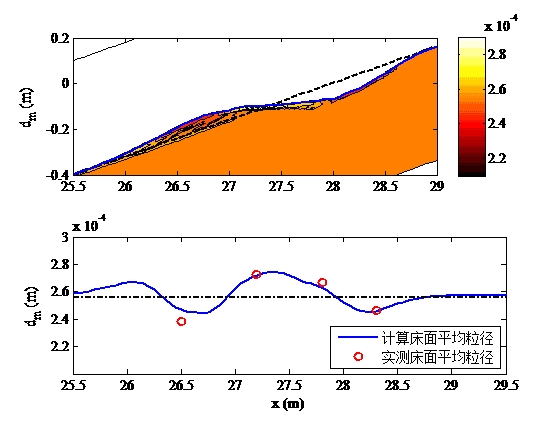
图4 床沙粒径分选模拟

图5 风暴和常浪作用下的沙坝双向迁移过程模拟

图6 水下人工沙坝的形态演变模拟及其消浪护滩效果分析
相关文献:
[1] Zheng, J. H., Zhang, C., Demirbilek, Z., & Lin, L. (2014). Numerical Study of Sandbar Migration under Wave-Undertow Interaction. Journal of Waterway, Port, Coastal and Ocean Engineering, 140(2), 146-159. (2014 Best Journal Paper Award)
[2] Zhang, C., Zhang, Q. Y., Zheng, J. H., & Demirbilek, Z. (2017). Parameterization of nearshore wave front slope. Coastal Engineering, 127, 80-87.
[3] Zhang, C., Zhang, Q. Y., Lei, G., Cai, F., Zheng, J. H, & Chen, K. F. (2018). Wave Nonlinearity Correction for Parametric Nearshore Wave Modelling. Journal of Coastal Research, 85(SI), 1-5.
[4] Zhang, C., Li, Y., Cai, Y., Shi, J., Zheng, J. H., Cai, F., Qi, H. S. (2019). Parameterization of nearshore wave breaker index. Coastal Engineering, (in revision).
[5] 张弛. 沙质海岸横向泥沙输运动力机制与数值模拟. 河海大学出版社, 南京, 中国. 2010. [ISBN 978-7-5630-2760-6/TV•308] [6] Zhang Chi, Zheng Jinhai and Zhang Jisheng. Predictability of wave-induced net sediment transport using the conventional 1DV RANS diffusion model. Geo-Marine Letters, 2014, 34(4): 353-364.
[7] Zhang Chi, Zheng Jinhai, Wang Yigang, Jeng Dong-Sheng and Zhang Jisheng. A process-based model for sediment transport under various wave and current conditions. International Journal of Sediment Research, 2011, 26(4): 500-514.
[8] Zhang Chi, Zheng Jinhai, Wang Yigang and Demirbilek Zeki. Modeling wave-current bottom boundary layers beneath shoaling and breaking waves. Geo-Marine letters, 2011, 31(3): 189-201.
[9] Zhang Chi, Zheng Jinhai, Wang Yigang, Zhang Mengtao, Jeng Dong-Sheng and Zhang Jisheng. Comparison of turbulence schemes for prediction of wave-induced near-bed sediment suspension above a plane bed. China Ocean Engineering, 2011, 25(3): 395-412.
[10] Zhang Chi, Wang Yigang and Zheng Jinhai. Numerical study on vertical structures of undertow inside and outside the surf zone. Acta Oceanologica Sinica, 2009, 28(5): 103-111.
[11] 李诚, 张弛*, 隋倜倜. 浅化波浪层流边界层流速分布特性的数值分析. 海洋学报, 2016, 38(5): 141-149.
[12] 吴丹, 张弛*. 随机波浪边界层的数值模拟与分析. 水动力学研究与进展(A辑), 2016, 31(3): 303-310.
[13] 张弛, 劳伯村, 郑金海. 加速度不对称波浪作用下的底部边界层动力特性. 河海大学学报(自然科学版), 2016, 44(3): 258-264.
[14] 张弛, 郑金海, 王义刚. 波浪作用下沙坝剖面形成过程的数值模拟[J]. 水科学进展, 2012, 23(1): 107-112.
[15] 张弛, 王义刚, 郑金海. 波生流垂向结构研究综述. 水科学进展, 2009, 20(5): 747-754.